Radio Horizon

h=Height of aerial above sea level
r=Radius of the earth (3440 Nautical miles)
d=Distance to Horizon
Using Pythagoras d²=(r+h)²-r²
hence d=√((r+h)²-r²)

Radio Horizon

To calculate the Radio Horizon because of refraction we achieve this by pretending the Earth has a larger radius which we call the equivalent Earth radius R_e which is normally 4/3r in the UK (4587 NM).
There are 6076 feet in a Nautical Mile

d_r=√((4587+h/6076)²-4587²)

The radio horizon between the transmitter and receiver is the addition of the horizon of both masts.

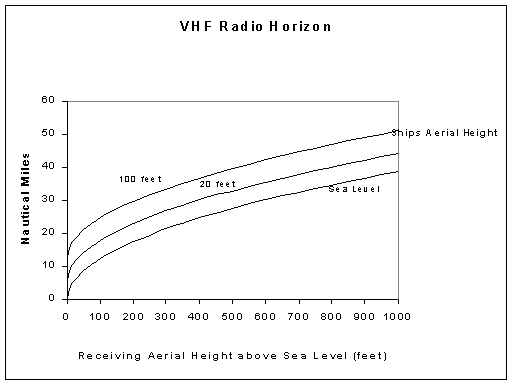
Note the size of the ship makes a considerable difference to the range.
Reception beyond this range is caused by propagation conditions and will be flukey.

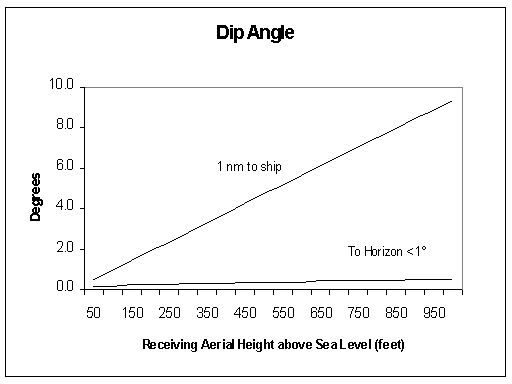
Dip

This was checked to see if a ship could actually be below the aerial horizon.
The graph shows the angle down to a ship for different receiving aerial heights. For a ship 1nm from the aerial and the aerial 1000 feet above sea level the angle down would be 10°. From the same aerial the horizon would be under 1°.


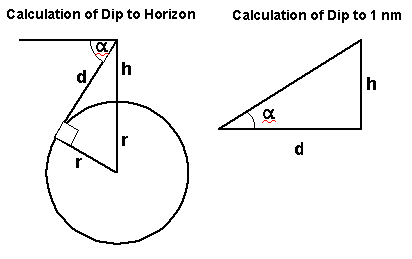
α=Dip angle
To Horizon sin(90-α)=r/(r+h)
To 1 nm tan α=h/d

 This significance is high gain collinear aerials increase horizontal gain at the expense of vertical beam width. The graph shows this could be relevant with a high gain aerial close to and much higher than the ship's aerial ie the ship is "below the radar"


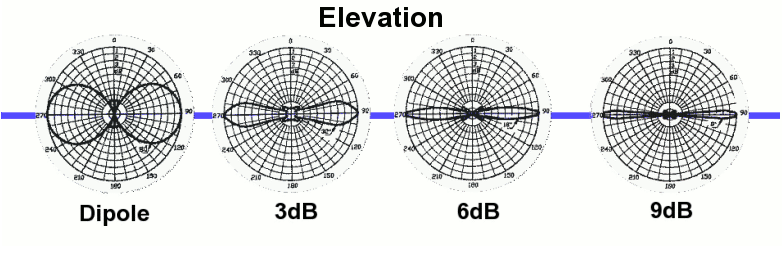
For example the Cushcraft Ringo Ranger specification quotes 7dBi gain and a beam width of  7 degrees. The dipole "donut" becomes a "biscuit" !
For more technical info see the references on my aerial page

See also
Beyond the Horizon Propagation & Tropospheric Ducting Forecast